Reduce data dimensionality without significant loss of information

As stated in the documentation for pre-factor analysis (see Multivariate > Factor > Pre-factor), the goal of factor analysis is to reduce the dimensionality of the data without significant loss of information. The tool tries to achieve this goal by looking for structure in the correlation matrix of the variables included in the analysis. The researcher will often try to link the original variables (or items) to an underlying factor and provide a descriptive label for each.

Example: Toothpaste

First, go to the Data > Manage tab, select examples from the Load data of type dropdown, and press the Load button. Then select the toothpaste dataset. The dataset contains information from 60 consumers who were asked to respond to six questions to determine their attitudes towards toothpaste. The scores shown for variables v1-v6 indicate the level of agreement with statements on a 7-point scale where 1 = strongly disagree and 7 = strongly agree.

Once we have determined the number of factors we can extract and rotate them. The factors are rotated to generate a solution where, to the extent possible, a variable has a high loading on only one factor. This is an important benefit because it makes it easier to interpret what the factor represents. While there are numerous algorithms to rotate a factor loadings matrix the most commonly used is Varimax rotation.

To replicate the results shown in the screenshot below make sure you have the toothpaste data loaded. Then select variables v1 through v6, set Nr. of factors to 2, and press the Estimate button or CTRL-enter (CMD-enter on mac) to generate results.

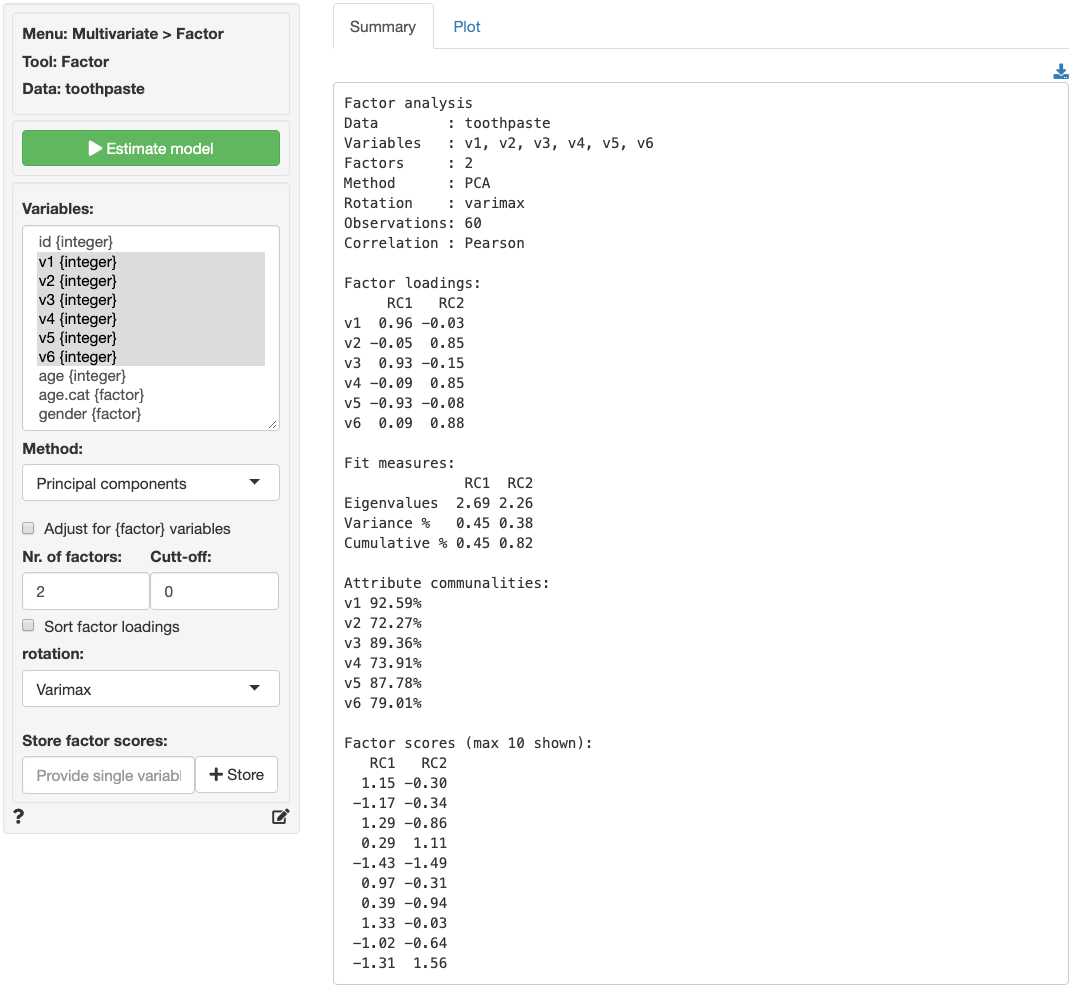
The numbers in the Factor loadings table are the correlations of the six variables with the two factors. For example, variable v1 has a correlation of .96 with factor 1 and a correlation of -.03 with factor 2. As such v1 will play a big role in naming factor 1 but an insignificant role in naming factor 2.

The rotated factor loadings can be used to determine labels or names for the different factors. We need to identify and highlight the highest factor loading, in absolute value, in each row. This is easily done by setting the Cut-off value to .4 and checking the Sort factor loadings box. The output is shown below.

Loadings:
     RC1   RC2
v1  0.96
v5 -0.93
v3  0.93
v6        0.88
v4        0.85
v2        0.85

Together, the variables shown in each column (i.e., for each factor) help us to understand what the factor represents. Questions 1, 3, and 5 reflect the importance of health issues while questions 2, 4, and 6 reflect aesthetics issues (see the data description in the Data > Manage tab for a description of the variables). Plausible names for the factors might therefore be:

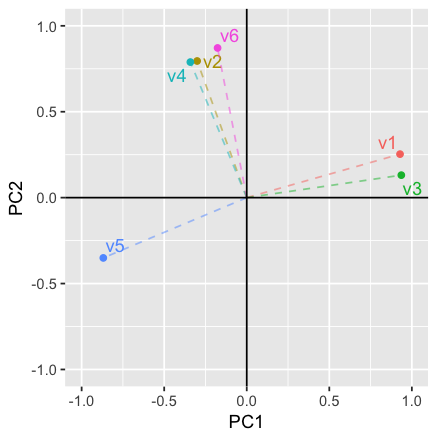
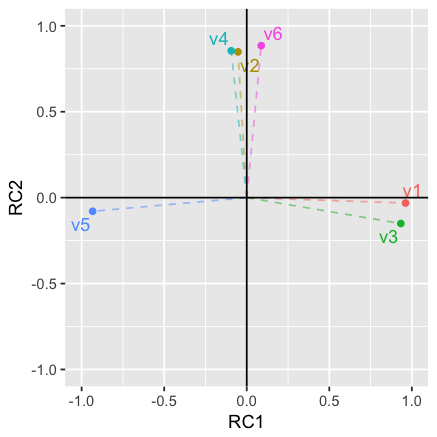
The best way to see what rotation does is to switch between Varimax and None in the Rotation dropdown and inspect what changes in the output after pressing the Estimate model button. Select None from the Rotation dropdown, switch to the Plot tab, and press the Estimate model button to see updated results. The image shown below depicts the loadings of the variables on the two factors. Variable v5 falls somewhat in between the axes for factor 1 and factor 2. When we select Varimax rotation, however, the label for v5 lines up nicely with the horizontal axis (i.e., factor 2). This change in alignment is also reflected in the factor loadings. The unrotated factor loadings for v5 are -0.87 for factor 1 and -0.35 for factor 2. The rotated factor loadings for v5 are -0.93 for factor 1 and -0.08 for factor 2.

The final step is to generate the factor scores. You can think of these scores as a weighted average of the variables that are linked to a factor. They approximate the scores that a respondent would have provided if we could have asked about the factor in a single question, i.e., the respondents inferred ratings on the factors. By clicking on the Store button two new variables will be added to the toothpaste data file (i.e., factor1 and factor2). You can see them by going to the Data > View tab. We can use factor scores in other analyses (e.g., cluster analysis or regression). You can rename the new variables, e.g., to health and social through the Data > Transform tab by selecting Rename from the Transformation type dropdown.

To download the factor loadings to a csv-file click the download button on the top-right of the screen.

Summary

  1. Determine if the data are appropriate for factor analysis using Bartlett, KMO, and Collinearity (Multivariate > Factor > Pre-factor)
  2. Determine the number of factors to extract using the scree-plot and eigenvalues > 1 criteria (Multivariate > Factor > Pre-factor)
  3. Extract the (rotated) factor solution to produce:
    • Factor loadings: Correlations between attributes and factors
    • Factor scores: Inferred ratings on the new factors (i.e., new variables that summarize the original variables)
  4. Identify the highest factor loading, in absolute value, in each row (i.e., for each variable)
  5. Label the factors using the strongest factor loadings

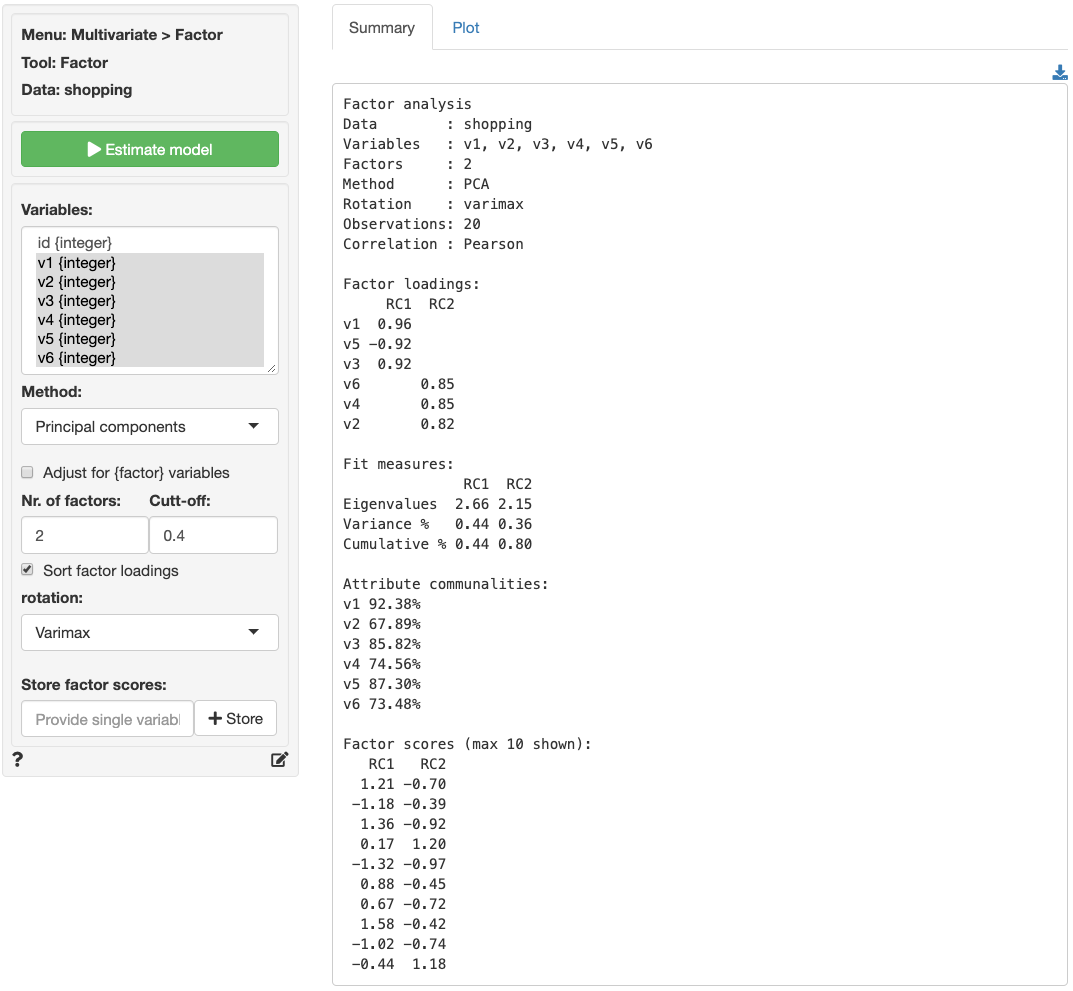
If you want more practice open the shopping data set and see if you can reproduce the results shown in the screen capture of the Summary tab below. Use Multivariate > Factor > Pre-factor to determine if the correct number of factors were selected. Do you agree? Why (not)?

Including categorical variables

Output shown in Multivariate > Factor is estimated using either Principal Components Analysis (PCA) or Maximum Likelihood (ML). The correlation matrix used as input for estimation can be calculated for variables of type numeric, integer, date, and factor. When variables of type factor are included the Adjust for {factor} variables box should be checked. When correlations are estimated with adjustment, variables that are of type factor will be treated as (ordinal) categorical variables and all other variables will be treated as continuous.

It is important to note that estimated factor scores will be biased if a mixed of {factor} and numeric variables are used. If you want to use factor scores as input for further analysis, e.g., clustering, you should use either (1) all {factor} variables or (2) all numeric variables to avoid this bias.

Report > Rmd

Add code to Report > Rmd to (re)create the analysis by clicking the icon on the bottom left of your screen or by pressing ALT-enter on your keyboard.

If a plot was created it can be customized using ggplot2 commands or with patchwork. See example below and Data > Visualize for details.

plot(result, custom = TRUE) %>%
  wrap_plots(plot_list, ncol = 2) + plot_annotation(title = "Factor Analysis")

R-functions

For an overview of related R-functions used by Radiant to conduct factor analysis see Multivariate > Factor.

The key functions from the psych packages used in the full_factor tool are principal and fa .

© Vincent Nijs (2024)